Neural networks may seem mysterious to most people, and thus theirs capabilities are often overestimated. However, in truth, any neural network is just a combination of elementary mathematical operations and in turn, a computational graph. In this post, I am going to show you to how to build a simple neural network with two layers for a classification problem and the math behind it. Part I here is about forward-propagation and the computational graph.

You may have heard people talk about neurons in neural networks, and it is a pretty neat way of describing dot products with non-linear transforms but that is not how we will look at our neural network. As can be seen above, the neural network is a graph that consists of vertices and edges. To put it simply, we can consider the states of the neural network (input, hidden state, and output) as vertices; the intermediate math operations can then be considered the edges of the graph. So overall, we have two types of edges:

• Fully connected layers
• Activations

The fully connected layer

The fully connected layer is nothing more than a matrix multiplication operation, usually with a bias vector added to the matrix multiplication output:

\[\mathbf{O} = \mathbf{IW+b},\]

where \(\mathbf{O}\) is the output vector of the fully connected layer, \(\mathbf{I}\) the input vector, \(\mathbf{W}\) the weight martrix, and \(\mathbf{b}\) the bias vector. Since it is a vector multiplied with a rectangular matrix, the fully connected layer is a set of dot products, with the input vector dotted with each column of the rectangular matrix \(\mathbf{W}\). The fully connected layer gets the name because every column vector is connected to the input vector.

Activations

Neural network activations are simply non-linear transforms, such as the hypertangent function. They are necessary because

• Multiple layers of unactivated matmul operations reduce to one
• Multiple layers of non-linear transforms are capable of approximating any complex function

Both of the above have been proven. In our case, we will use something called Rectified Linear Unit (ReLU):

\[\theta=max(0,x),\]

where \(\theta\) is the activated output and x the input. The ReLU function is simply a piecewise linear function:

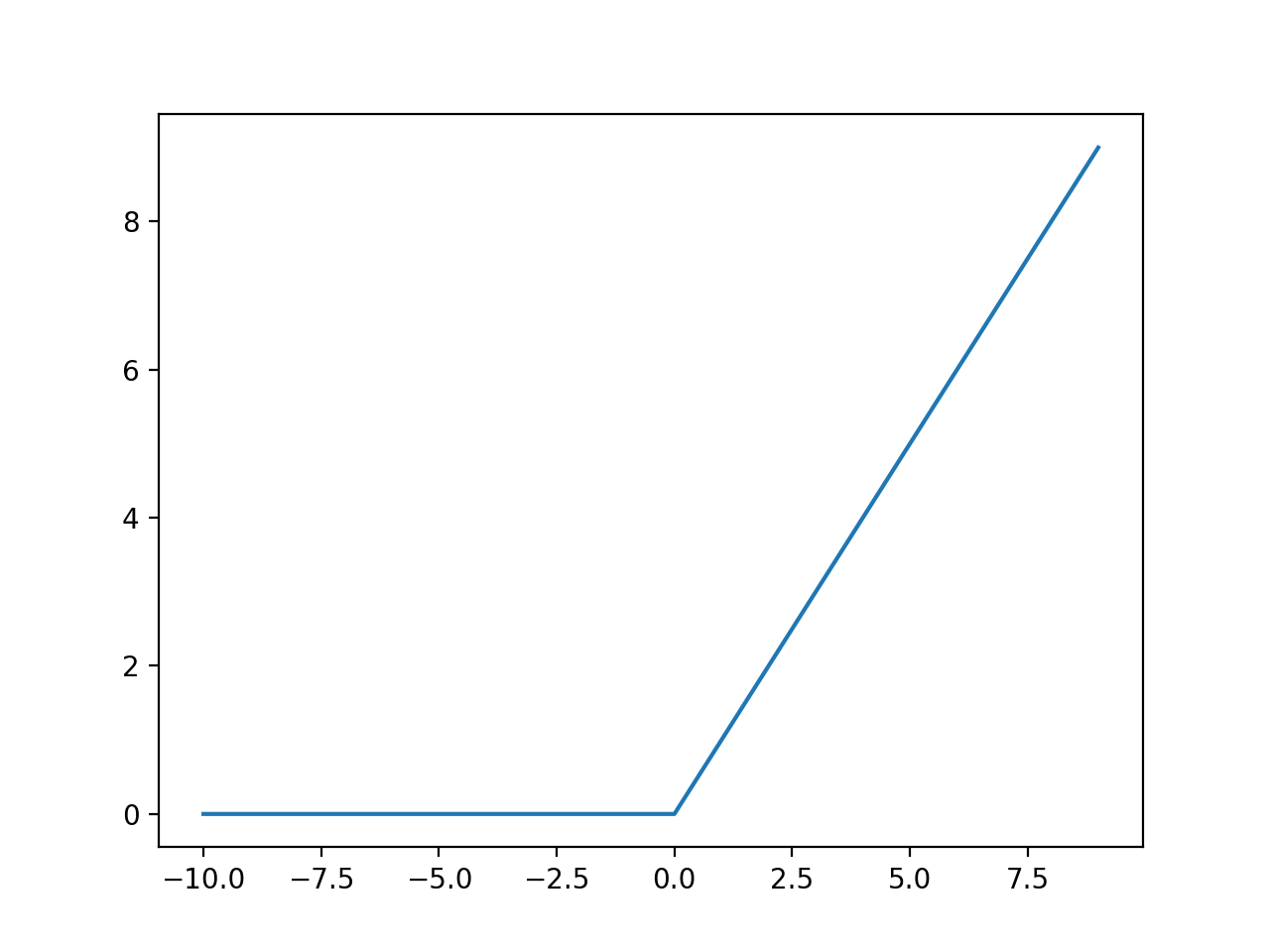
ReLU will be used to get the hidden state, while softmax will be used to transform the output from the fully connected layer to a set of probabilities:

\[\text{Softmax}(x_{i}) = \frac{\exp(x_i)}{\sum_j \exp(x_j)}.\]

The computational graph

Now that we have seen all components of our computational graph, let’s visualize it

In the end, the output is a set of probabilities for a classification problem. The largest probability is selected as the prediction. The graph above summarizes forward-propagation and how inference is done in our neural network. Now we see that the neural network is nothing but a set of elementary math operations.

It is easy to see that all intermediate math operations are readily differentiable, which means we can apply chain rule to propagate gradients throughout the entire network. Such gradient propagation is known as back-propagtion, which we will talk about in detail in part II. Keep in mind that back-propagation is how we train our neural network.